你还在为考试担忧吗?你还在为如何提高分数苦恼吗?出国留学网吧为你整理2017年经济师相关的资讯哦,欢迎广大考生前来学习,希望你能轻松过考!
【考点二】算术平均数、几何平均数
(一)算数平均数的特点、适用范围
建议关注算术平均数的计算方法、几何平均数的用途。
定义 | 是全部数据的算术平均,又称均值,用 表示。 |
特点 | (1)是集中趋势最主要的测度值。 |
适用范围 | 主要适用于数值型数据,但不适用于品质数据。 |
(二)两种算数平均数的比较
简单算术平均数 | 加权算术平均数 | |
计算方法 | 设一组数据为X1,X2,…,Xn,计算公式为: #FormatImgID_0# | 设原始数据被分成k组:各组的组中值为X1,X2,…,Xk,各组的频数分别为f1,f2,…,fk,计算公式为: |
适用范围 | 用于处理未分组的原始数据 | 用于处理经分组整理的数据 |
【例如】某售货小组有5名营业员,元旦一天的销售额分别为520元、600元、480元、750元和500元,求该日每名营业员的平均销售额。
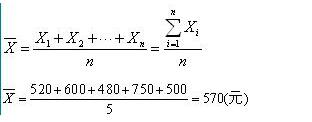
【例如】某市商业企业协会根据100个会员样本,整理出一年销售额分布资料:
销售额分布资料
销售额(万元) | 组中值 | 商业企业数fi | Xifi |
100-150 | 125 | 4 | 500 |
150-200 | 175 | 16 | 2800 |
200-250 | 225 | 40 | 9000 |
250-300 | 275 | 28 | 7700 |
300-350 | 325 | 10 | 3250 |
350-400 | 375 | 2 | 750 |
合计 | — | 100 | 24000 |
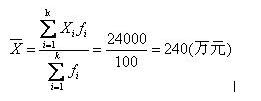
(三)几何平均数
1.n个观察值连乘积的n次方根就是几何平均数。
2.简单几何平均数的计算。
设一组数据为X1,X2,…,Xn,且大于0, 表示几何平均数,则:
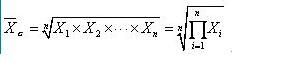
式中,∏为连乘积符号。
计算几何平均数要求各观察值之间存在连乘积关系,它的主要用途是:(1)对比率、指数等进行平均。(2)计算平均发展速度。
【例如】某型号钻头的生产,需经过6道不同的加工工序,各道工序的合格率下表所示,计算平均合格率。
各道加工工序合格率
工序名称 | 合格率(%) |
冲料 | 98.2 |
料废 | 97.5 |
车工 | 97.0 |
加热 | 96.6 |
扫槽 | 95.5 |
接柄 | 95.0 |
用几何平均数的方法进行计算,得:
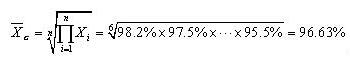
【例题·单选题】(2013年)某产品的生产需经过8道不同的加工工序,根据各道工序的合格率计算该产品的平均合格率,应使用( )。
A.算术平均数
B.中位数
C.众数
D.几何平均数
『正确答案』D
『答案解析』计算几何平均数要求各观察值之间存在连乘积关系,它的主要用途是:(1)对比率、指数等进行平均。(2)计算平均发展速度。
【总结】集中趋势指标特点总结
指标 | 极端值 | 品质数据 | 数值型数据 | ||
分类数据 | 顺序数据 | ||||
位置平均数 | 众数 | 不受影响 | 适用 | 适用 | 适用 |
中位数 | 不适用 | 适用 | 适用 | ||
数值平均数 | 算术平均数 | 受影响 | 不适用 | 不适用 | 适用 |
几何平均数 | 不适用 | 不适用 | 连乘积关系的适用 | ||

